최소 신장 트리 - 프림 알고리즘, 크루스칼 알고리즘

이 글은 기술면접대비 CS전공 핵심요약집의 일부분인 알고리즘 부분의 내용을 가져와 작성하였습니다.
구글 도서 검색 을 통해 전체 페이지 240 중 102페이지를 미리보기 하실 수 있습니다.
개인적으로 아래 내용은 위키 백과를 함께 보시길 권장 드립니다.
신장 부분 그래프, 프림 알고리즘, 크러스컬 알고리즘

최소 신장 트리 (MST, Minimium Spanning Tree)

신장 트리는 그래프의 모든 정점을 포함하는 트리를 의미한다. 그중에서 최소 신장 트리는 가중치가 있는 그래프에서 간선의 가중치 총합이 가장 작은 신장 트리를 의미한다.

주로 코딩 테스트에서 가중치가 있는 그래프에 대해 최소 신장 트리를 찾는 문제로 등장한다.

프림 알고리즘 (Prim algorithm)

프림 알고리즘은 그리디 알고리즘으로, 임의의 정점을 시작점으로 트리를 확장하면서 최소 신장 트리를 생성하는 방식이다. 현재 트리에 포함된 정점과 연결된 간선 중 가중치가 가장 작은 간선으로 연결된 정점을 선택하는 과정을 반복하며 모든 정점이 포함될 때까지 트리를 확장한다.

그리디 알고리즘 (greedy algorithm) 탐욕 알고리즘이라고도 하며, 각 단계에서 최선의 선택이 모여 전역으로 최적의 해결 방안을 찾는 방식이다. 그리디 알고리즘은 아래 두 가지 조건을 만족해야 한다.
1. 앞에서 선택한 결과가 나중의 선택에 영향을 주지 않아야 한다.
2. 지역적인 문제에 대한 최선의 선택이 전역적인 문제에 대해서도 최적의 해여야 한다.

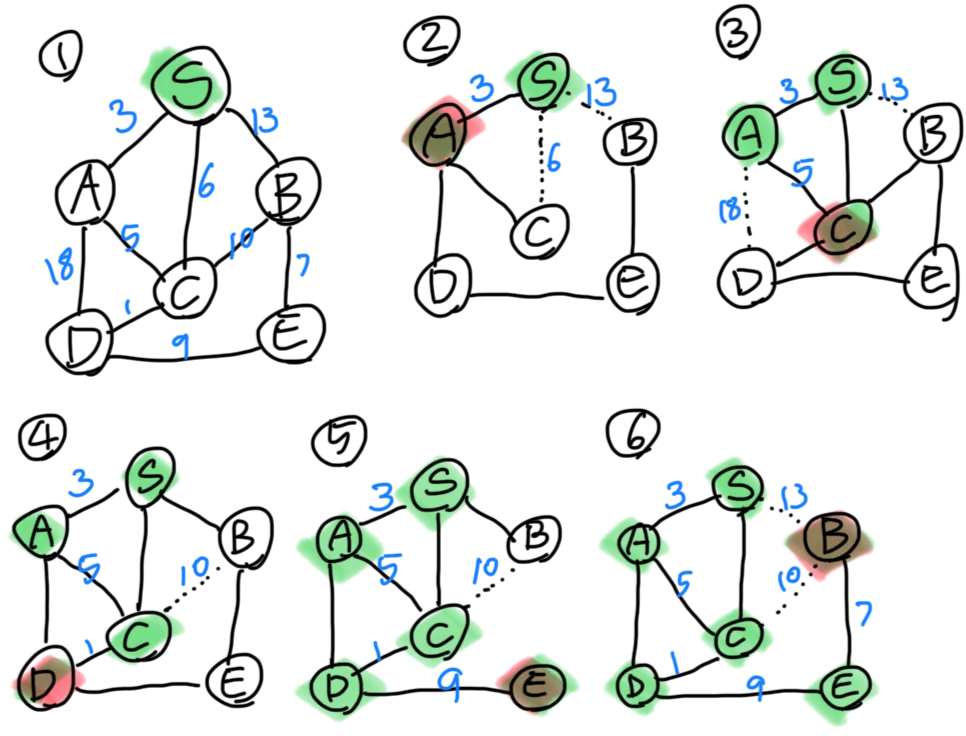
1. 최소 신장 트리를 찾을 그래프로, 시작 정점은 S
2. 정점 S에서 탐색 가능한 정점은 A, B, C. 각 정점은 각각 가중치 3, 6, 13인 간선과 연결되어 있다. 이 중에서 가장 작은 가중치인 3인 간선에 연결된 정점 A를 트리에 추가한다.
3. 정점 S와 A에서(트리에서) 탐색 가능한 정점은 B, C, D. 각 정점과 연결된 간선의 최소 가중치는 13, 5, 18이다. 이 중에서 가장 작은 가중치인 5인 간선으로 연결된 C를 트리에 추가한다.
4. 정점 S와 A 그리고 C에서 탐색 가능한 정점은 B와 D이고, 각 정점과 연결된 간선의 최소 가중치는 10과 1이다. 이 중에서 가장 작은 가중치인 1인 간선과 연결된 정점 D를 트리에 추가한다.
5. 정점 S, A, C, D에서 탐색 가능한 정점은 B와 E. 연결된 간선의 최소 가중치는 10과 9이다. 이 중에서 가장 작은 가중치는 9이며 연결된 정점인 E를 트리에 추가한다.
6. 정점 S, A, C, D, E에서 탐색 가능한 정점은 B이며 연결된 간선 중 최소 가중치 7인 간선을 선택해 정점 B를 트리에 추가한다. 이로써 모든 정점이 트리에 포함되어 최소 신장 트리가 완성된다.
7. 프림 알고리즘은 가중치가 가장 작은 간선으로 연결된 정점을 트리에 추가하면서 최소 신장 트리를 생성한다.

크루스칼 알고리즘 (Kruskal algorithm)

크루스칼 알고리즘도 그리디 알고리즘이며, 간선을 오름차순으로 정렬 한 뒤 가중치가 가장 낮은 간선을 선택하면서 최소 신장 트리를 생성하는 방식이다. 만약 특정 간선을 선택했을 때 사이클이 생성된다면 해당 간선은 선택하지 않고 다음으로 가중치가 낮은 간선을 확인한다. 이 과정을 반복하다가 모든 정점이 연결되면 알고리즘을 종료한다. 크루스칼 알고리즘에서는 가중치의 오름차순으로 간선을 정렬하는 알고리즘과, 사이클의 생성 여부를 판단하는 유니온 파인드(union-find) 알고리즘을 함께 사용한다.

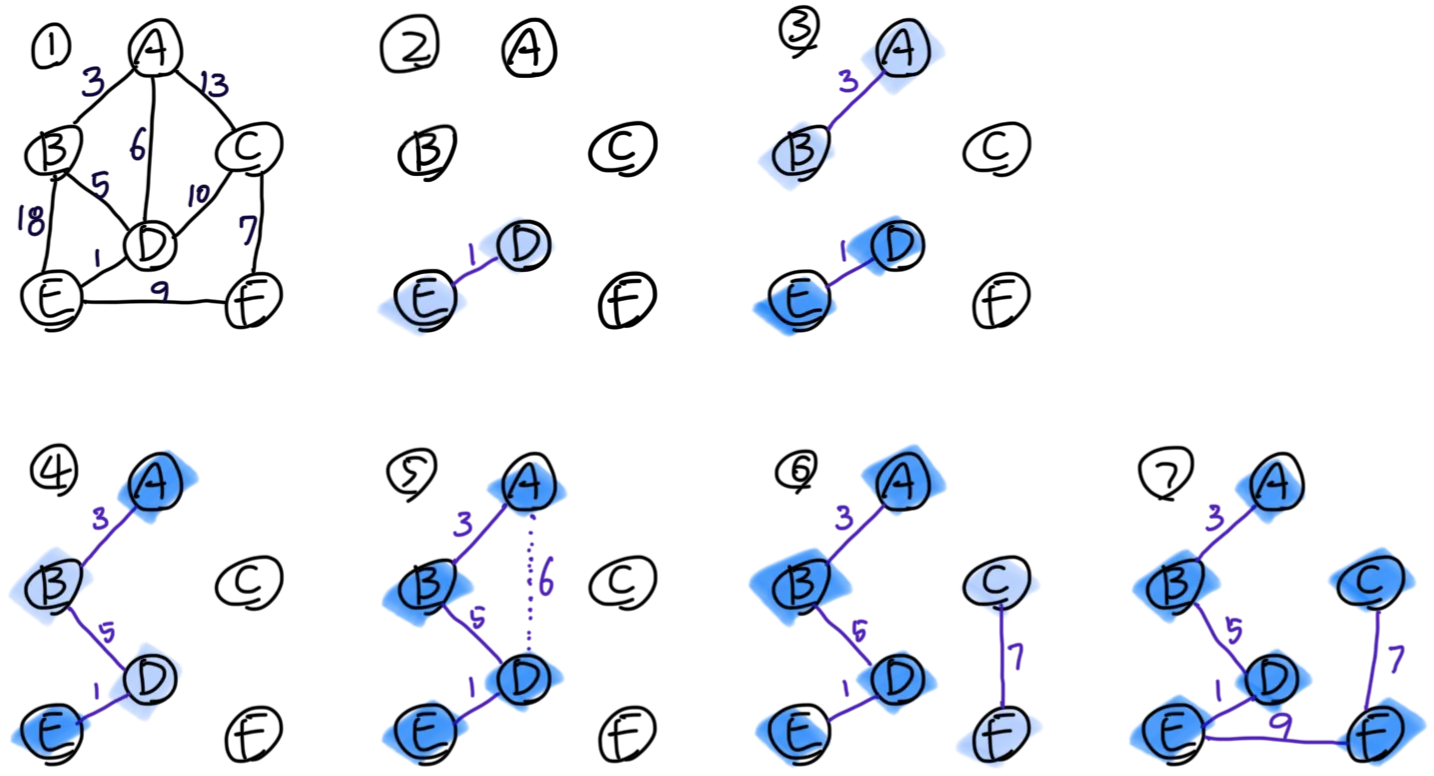
1. 최소 신장 트리를 구하기 위한 그래프로, 간선의 가중치가 각각 다르다.
2. 전체에서 가중치가 1로 가장 작으면서 정점 D와 E를 연결하는 간선을 선택한다.
3. 가중치가 다음으로 작은 가중치 3인 간선을 선택한다. 이 간선은 정점 A와 B를 연결한다.
4. 가중치가 그다음으로 작은 가중치 5인 간선을 선택한다. 이 간선은 정점 B와 D를 연결한다.
5. 가중치가 그 다음으로 작은 간선은 정점 A와 D를 연결하는 가중치 6인 간선이다. 이 간선을 트리에 포함하면 정점 A, B, D 사이에 사이클이 형성되므로 선택할 수 없다.
6. 가중치가 다음으로 작은 간선을 찾는다. 정점 C와 F를 연결하는 간선이 가중치 7이므로 해당 간선을 선택한다.
7. 가중치가 그다음으로 작은 간선은 정점 E와 F를 연결하는 가중치 9 간선이다. 이 간선을 선택하면 모든 정점이 연결되므로 최소 신장 트리가 완성된다.

예에서 보듯 크루스칼 알고리즘은 정점을 기준으로 트리를 생성하는 프림 알고리즘과 달리 간선을 기준으로 트리를 생성한다. 즉, 흩어져 있는 여러 트리(노드)를 가중치가 작은 간선으로 연결해 하나의 최소 신장 트리를 생성한다.

유니온 파인드 알고리즘
유니온 파인드는 2개의 원소가 같은 집합에 속하는지 판단하는 알고리즘으로, 그래프에서 2개의 노드가 같은 그래프에 속하는지 판별할 수 있다. 그래프에는 루트 노드가 없기 때문에 대표 노드를 설정해 그래프를 구분한다. 유니온은 두 노드를 하나의 그래프로 합치는 연산을, 파인드는 특정 노드가 속한 그래프의 대표 노드를 찾는 연산을 의미한다. 크루스칼 알고리즘에서는 사이클 발생을 방지하기 위해 유니온 파인드 알고리즘을 사용한다. 두 정점을 선택하고 유니온 파인드 알고리즘을 통해 다른 그래프에 속한다고 판별되면 두 정점을 연결하고, 같은 그래프에 속한다고 판별되면 두 정점을 연결하지 않는다.